Simplifying Radical Expressions
for all real numbers
if both x and y are non-negative, and
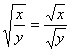if both x and y are non-negative, and y is not zero
WARNING:
Never cancel something inside a radical with something outside of it:
WRONG! If you did this you would be canceling a 3 with
, and they are certainly not the same number.
The general plan for reducing the radicand is to remove any perfect powers. We are only considering square roots here, so what we are looking for is any factor that is a perfect square. In the following examples we will assume that x is positive.
Example:
In this case the 16 was recognized as a perfect square and removed from the radical, causing it to become its square root, 4.
Example:
Although x3 is not a perfect square, it has a factor of x2, which is the square of x.
Example:
Here the perfect square factor is x4, which is the square of x2.
Example:
In this example we could take out a 4 and a factor of x2, leaving behind a 2 and one factor of x.
· The basic idea is to factor out anything that is “square-rootable” and then go ahead and square root it.